Bài toán của thầy Văn Như Cương khó cỡ nào mà đến GS Ngô Bảo Châu cũng phải đau đầu tìm lời giải?

GS Ngô Bảo Châu là một nhà toán học Pháp - Việt nổi tiếng khi thành công trong việc chứng minh bổ đề cơ bản cho các dạng tự đẳng cấu. Ông đã làm rạng danh nền Toán học nước nhà khi là người Việt Nam đầu tiên và duy nhất đạt Huy chương Fields vào năm 2010 nhờ thành công này. Mới đây, giáo sư gây chú ý khi chia sẻ lại bài toán "hóc búa" của thầy Văn Như Cương - nhà giáo Việt Nam, nhà biên soạn sách giáo khoa phổ thông và giáo trình đại học bộ môn hình học - trên trang Facebook cá nhân có hơn 300.000 người theo dõi kèm lời "than thở": "Đây là bài toán thầy Văn Như Cương đặt ra cho kỳ thi IMO một năm nào đó (1982 - PV). Bài toán rất hay, mình nghĩ ung thủ mới ra. Đề nghị các bạn thích toán đố thử giải. Cấm google!". 

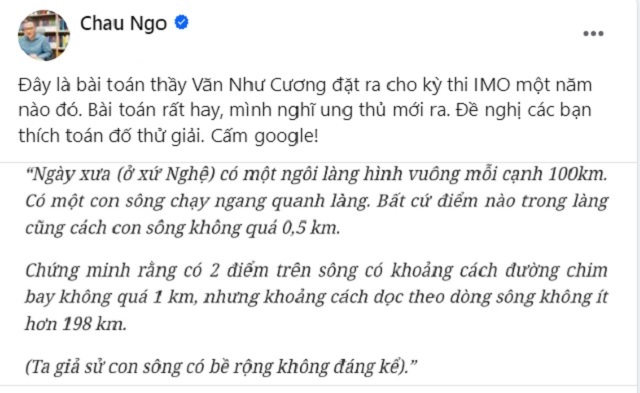
Đến giáo sư Toán học tầm cỡ quốc tế còn phải "nhức đầu" khi giải bài toán của thầy Cương thì chắc hẳn độ khó của nó không có gì để bàn cãi nữa. Được biết, bài toán này nằm trong đề thi Olympic Toán quốc tế (IMO) năm 1982. Thời điểm đó, nhiều quốc gia đã muốn loại nó ra khỏi đề thi vì cho rằng quá khó đối với các thí sinh tham gia. Cuối cùng bài toán của thầy Cương vẫn được giữ lại vì giáo sư, viện sĩ người Hungary tên R. Alfred cũng là Chủ tịch IMO cho rằng nó rất hay, còn không tiếc lời khen ngợi. Tuy nhiên để "vừa sức" với thí sinh thì điều kiện của bài toán đã được chỉnh sửa cho dễ hơn. 

*Nội dung gốc của bài toán là: "Ngày xưa (ở xứ Nghệ) có một ngôi làng hình vuông mỗi cạnh 100km. Có một con sông chạy ngang quanh làng. Bất cứ điểm nào trong làng cũng cách con sông không quá 0,5km. Chứng minh rằng có 2 điểm trên con sông có khoảng cánh đường chim bay không quá 1km nhưng khoảng cách dọc theo dòng sông không ít hơn 198km (Ta giả sử con sông có bề rộng không đáng kể)".

*Nội dung bài toàn sau khi chỉnh sửa: "Cho hình vuông S có độ dài cạnh là 100. L là một đường gấp khúc không tự cắt tạo thành từ các đoạn thẳng A0A1, A1A2…, A(n-1)An với A0 ≠ An. Giả sử với mỗi điểm P nằm trên chu vi của S đều tồn tại một điểm thuộc L cách P không quá 1/2. Chứng minh rằng: Tồn tại hai điểm X và Y thuộc L sao cho khoảng cách giữa X và Y không vượt quá 1, và độ dài đường gấp khúc L nằm giữa X và Y không nhỏ hơn 198".

Trong kỳ thi  Olympic Toán quốc tế năm đó, số thí sinh giải được bài toán (đã chỉnh sửa) chỉ có 20 người. Một trong số đó chính là thí sinh Việt Nam Lê Tự Quốc Thắng. Anh đạt số điểm 42/42, giành Huy chương Vàng và góp phần nâng thứ hạng của Đoàn Việt Nam lên vị trí 5/30 quốc gia tham dự.